招聘小程序搭建教程
本文共 646 字，大约阅读时间需要 2 分钟。
微搭低代码平台的模板中心提供了丰富的行业模板，日常我们在开发小程序时可以作为重要的参考来源。对于新入局的玩家，看懂官方的模板并熟练应用无疑是学习的捷径，今天博主就带着大家熟悉一下官方提供的这套招聘小程序的模板。
扫码体验
官方的模板可以用手机直接扫码体验，我们拆解一下都有哪些功能
候选列表
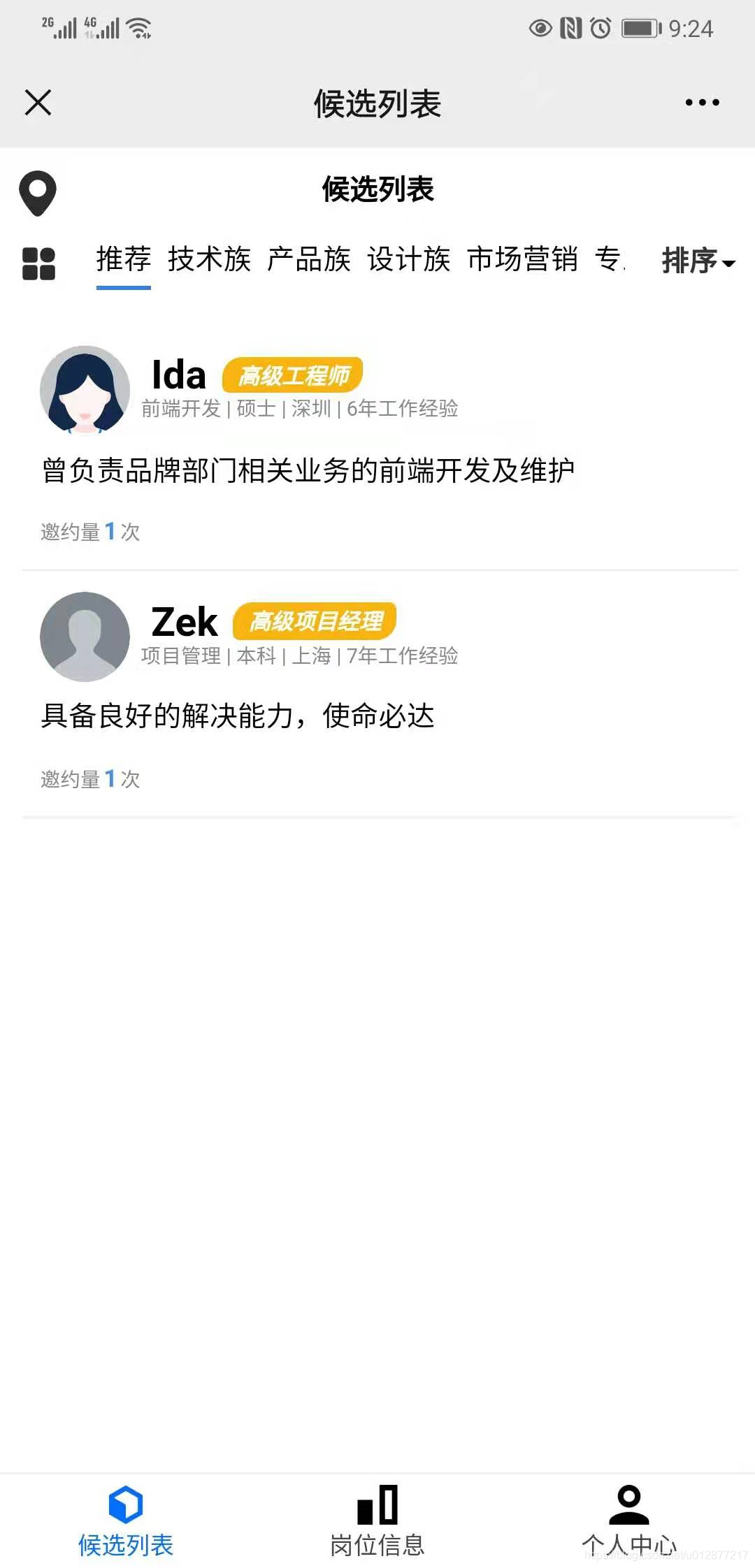
看到页面我们可以拆分成功能点 - 可以切换区域
- 可以按照类别浏览候选人
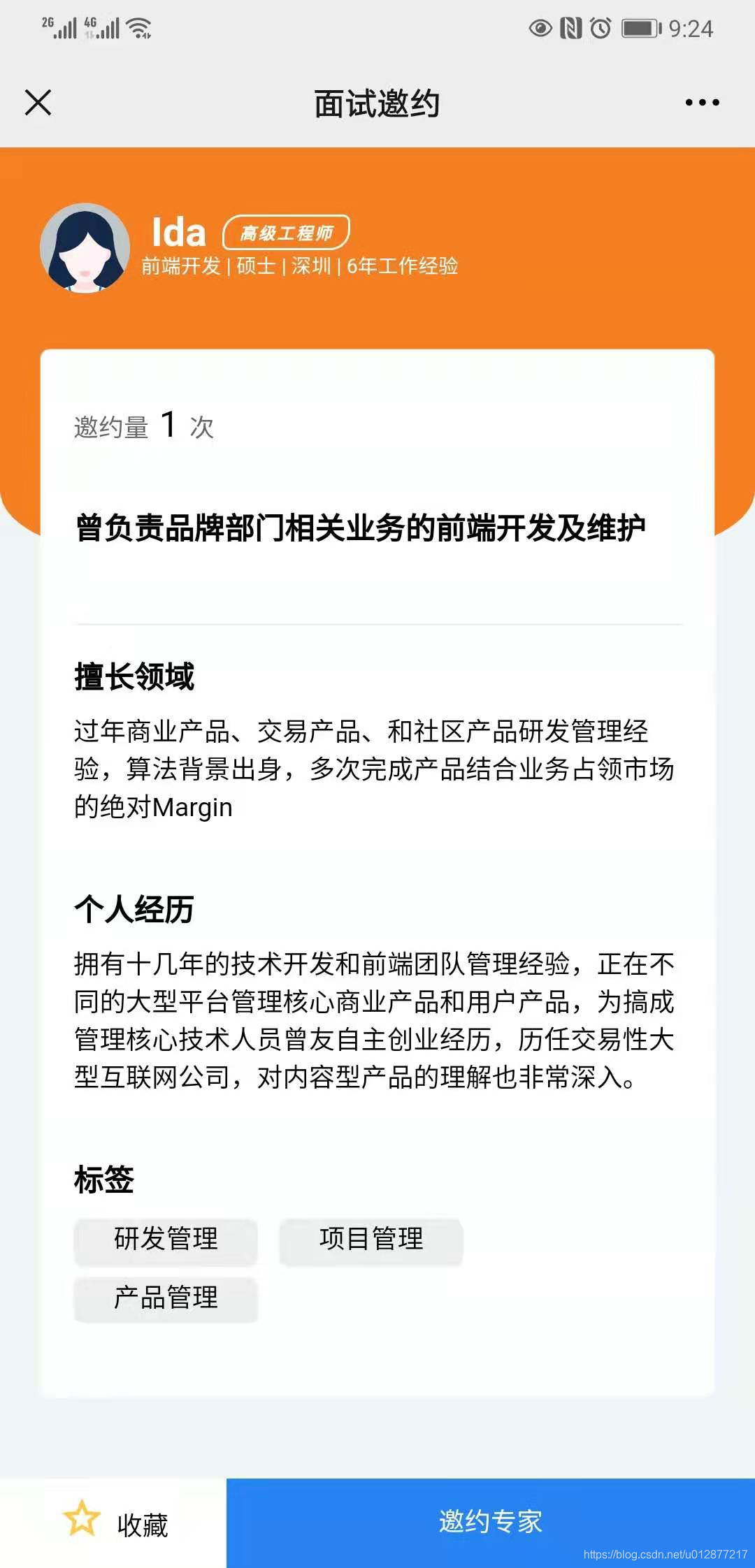
- 可以查看候选人详情
- 可以进行面试邀约
- 可以收藏
- 可以进行排序
岗位信息
同样也拆分出功能点 - 可以按照类别浏览岗位信息
- 可以查看岗位的详情
个人中心
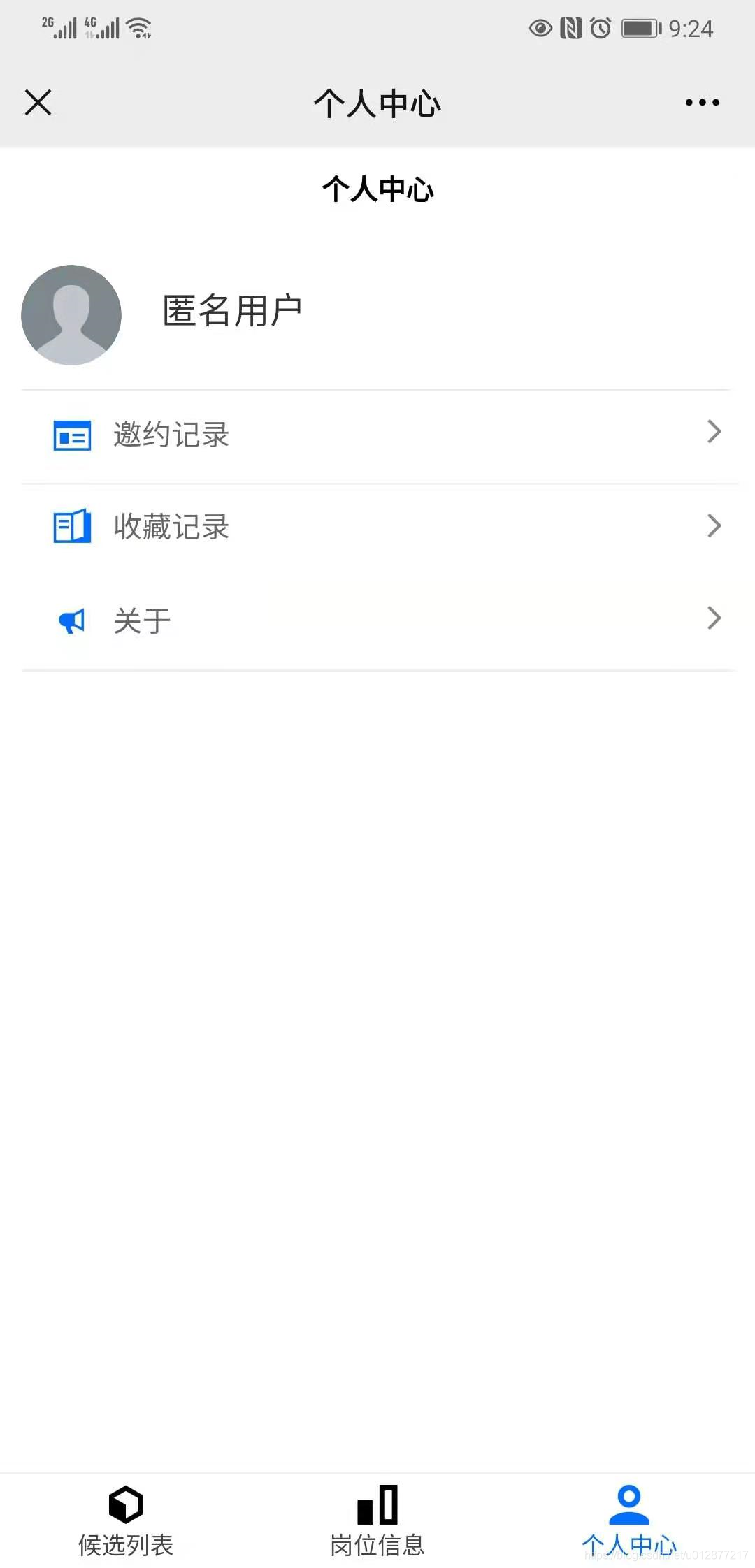
同样也拆分一下功能点 - 可以进行登录
- 可以查询邀约的记录
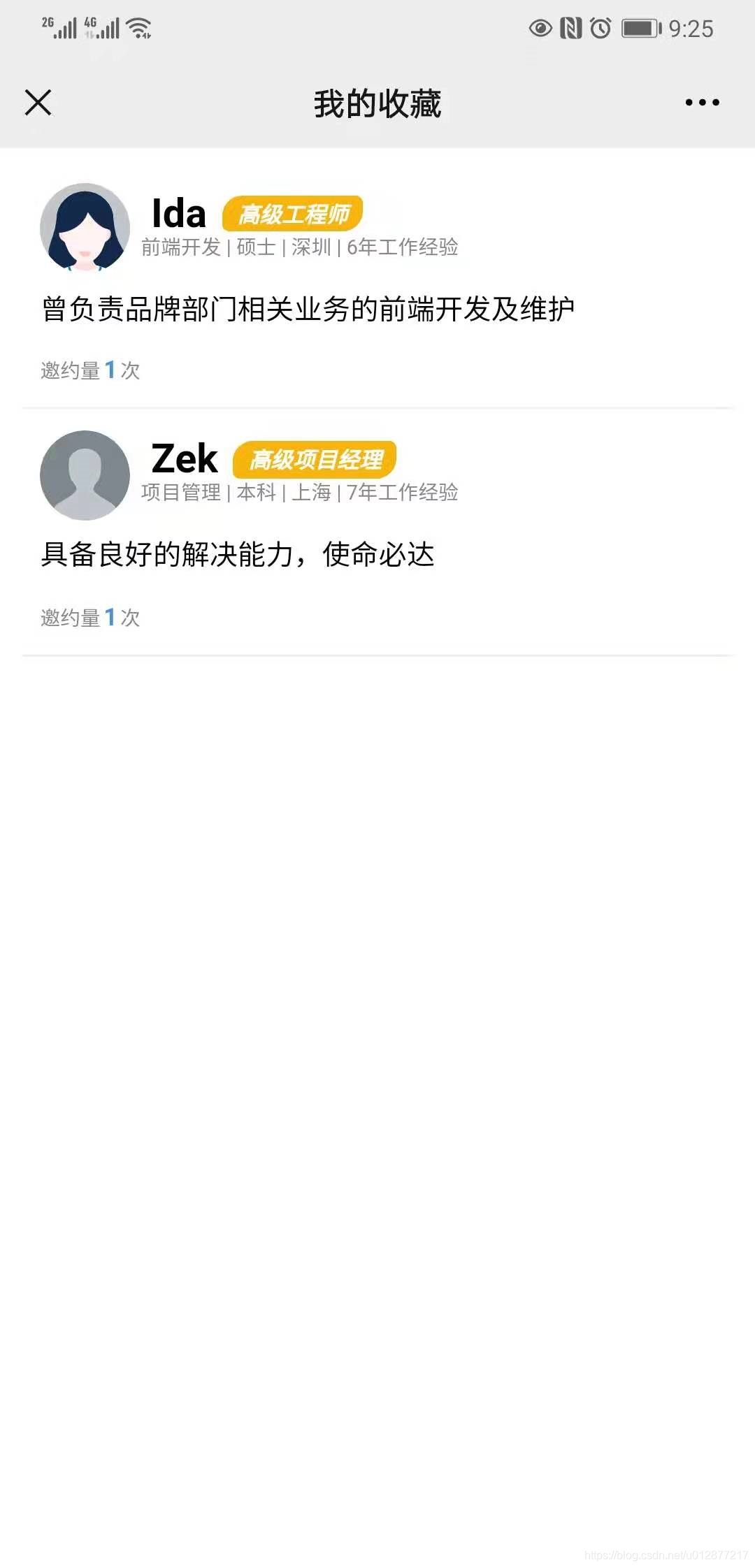
- 可以查询收藏的记录
- 可以查看平台介绍
功能设计
我们拆分了功能点之后，一般是需要规划一下有多少个页面，我们看一下下载下来的模板
| 页面标识 | 页面名称 |
|---|---|
| index | 候选列表 |
| graph | 岗位信息 |
| user | 个人中心 |
| graph | 岗位信息 |
| about | 关于 |
| expertDetail | 面试邀约 |
| classification | 全部分类 |
| invacations | 我的邀约 |
| favorites | 我的收藏 |
| category | 分类查看 |
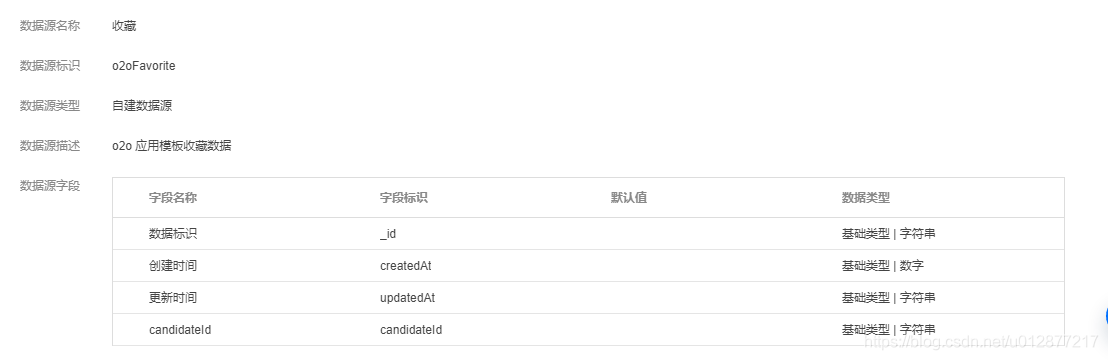
数据源
页面分析完毕之后我们看一下模板创建的数据源，一共是创建了四个数据源
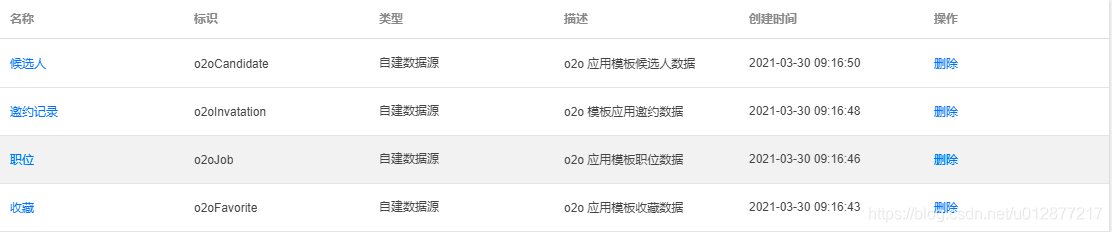
候选人
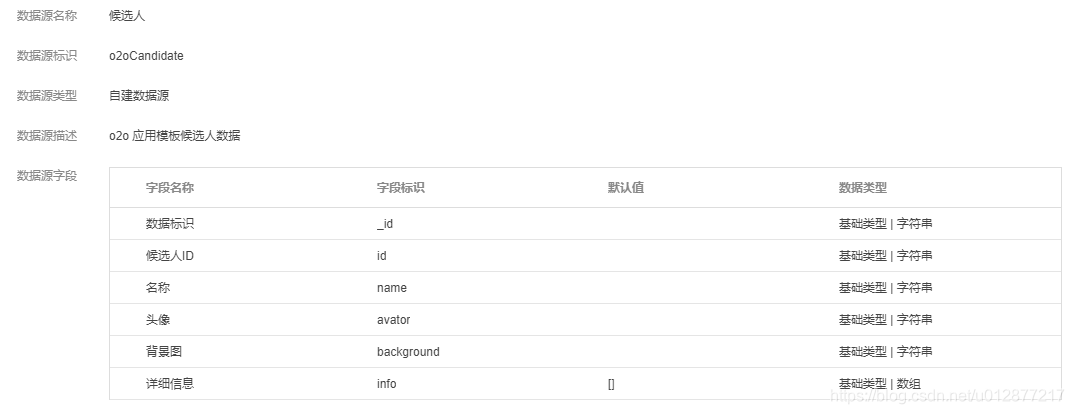
邀约记录
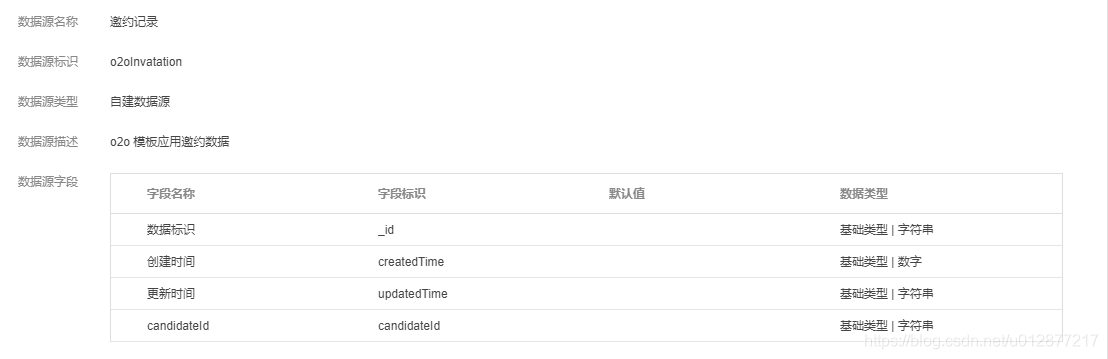
职位
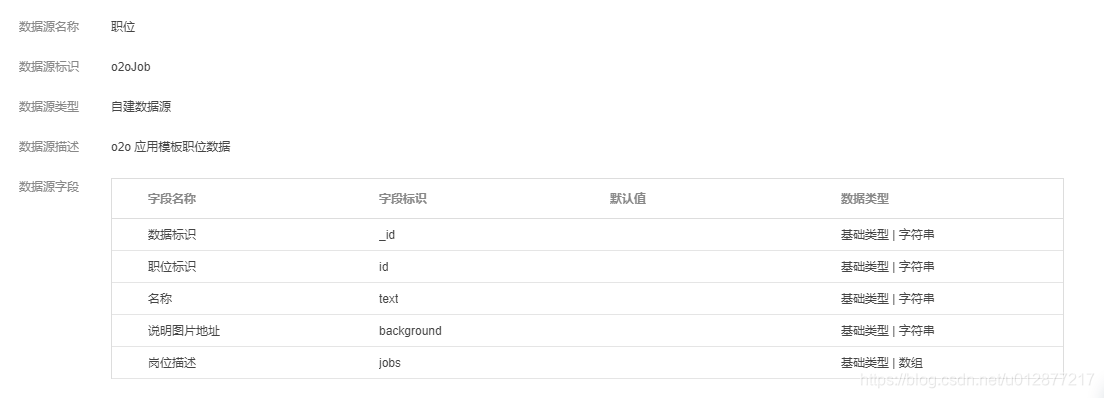
收藏
模板总结
官方提供的这套模板总体还是比较复杂的，基本涵盖了小程序需要使用的大多数功能，当然有不少人也质疑低码只能做一些简单的表单应用，这套模板我觉得无疑就是有力的证明，只要你下功夫复杂的也是可以做到的。
转载地址：http://lpbzz.baihongyu.com/
你可能感兴趣的文章